最佳投資組合怎麼找？效率前緣教你報酬與風險的黃金平衡｜現代投資組合理論（五）

為什麼「最佳投資組合」不是憑感覺？

2024年初，台北某投資社團裡，一位資深股民分享他的「完美組合」：70%台積電、20%聯發科、10%鴻海。他的理由很直接：「台積電最強，聯發科有潛力，鴻海便宜，這樣分散風險又能賺錢。」底下留言一片讚賞，但也有人提出疑問：「為什麼是70%、20%、10%？不是80%、15%、5%？」

這個簡單的問題，揭露了多數投資人的盲點：我們憑什麼認為某個配置比例是最好的？

大部分投資人在配置資產時，都是靠「感覺」：覺得某檔股票會漲就多買一點，覺得風險太高就分散一下。但這種方法存在三個根本問題：

主觀性過強：每個人的「感覺」不同，沒有客觀標準
缺乏數學基礎：無法量化風險與報酬的真實關係
優化程度有限：可能錯過更好的配置組合

在我們前四篇文章中，已經建立了現代投資組合理論的基礎：時間價值計算教我們理解投資的必要性，風險量化方法讓我們精確衡量風險，相關係數分析揭示了分散投資的數學原理。

今天，我們要用這些工具解決投資的終極問題：如何在無數種配置選項中，找到數學上最有效率的投資組合？

答案就是：效率前緣。它不是憑感覺，而是用數學找到報酬與風險的黃金平衡點。

效率前緣的數學基礎

效率前緣(Efficient Frontier)是現代投資組合理論的核心概念，由諾貝爾經濟學獎得主Harry Markowitz在1952年提出。簡單來說，它是給定一組投資標的下，所有可能的「報酬-風險」組合點中，最有效率的那些點所形成的曲線。

什麼是「最有效率」？

想像你在挑選手機，有兩款規格：

• 手機A：性能80分，價格8000元
• 手機B：性能80分，價格10000元

理性的消費者一定選手機A，因為同樣性能下價格更低。手機B就是「無效率」的選擇。

投資組合也是同樣道理：

• 效率組合：在相同風險下，提供最高報酬；或在相同報酬下，承受最低風險
• 無效率組合：存在其他組合能在不增加風險的情況下提供更高報酬

數學計算基礎與模型約束

本文均以 w≥0、∑w=1 為約束，不含槓桿與賣空；加入無風險資產後將導出資本市場線與切線組合（第六篇）。

還記得我們在前幾篇學過的公式嗎？現在它們要派上用場了。

組合預期報酬率（加權平均）：

μ_p = w₁μ₁ + w₂μ₂

組合風險（考慮相關係數）：

σ_p = √(w₁²σ₁² + w₂²σ₂² + 2w₁w₂σ₁σ₂ρ₁₂)

其中：

• w₁, w₂ = 各資產的投資權重
• μ₁, μ₂ = 各資產的預期報酬率
• σ₁, σ₂ = 各資產的標準差（風險）
• ρ₁₂ = 兩資產的相關係數

效率前緣的視覺化

效率前緣在圖表上呈現為一條向左上方彎曲的曲線，具有外凸（convex to the origin）的特性。外凸代表「1+1 可小於 2 的風險」——低相關資產組合能把風險拉到兩單一資產線性內插之下：

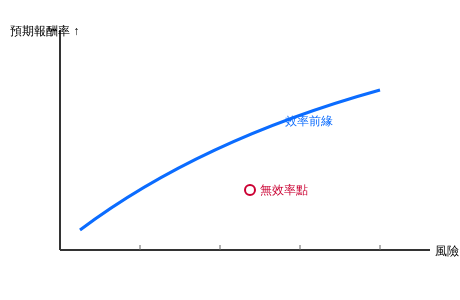
這條曲線有個重要特性：曲線上的每一點都是最佳選擇，曲線內部的點都是可以被改善的次優選擇。

投資組合的黃金平衡點

理論聽起來抽象，讓我們用台股投資人最熟悉的ETF來具體說明。

兩檔ETF的組合分析

假設我們要在元大台灣50（0050）和元大高息低波（00713）之間做資產配置：

個別表現（示例數據）：

• 100% 0050：預期年報酬9%，年化波動率22%
• 100% 00713：預期年報酬6%，年化波動率16%

註：以上參數僅為示例，用於說明計算方法。實際投資應使用最新的歷史數據計算。

直覺上，你可能認為任何組合的風險報酬都會落在這兩點之間。但效率前緣告訴我們，巧妙的投資組合優化可能創造意想不到的效率前緣效應。

60/40組合的效率前緣效應

讓我們計算60% 0050 + 40% 00713的組合（假設兩者相關係數為0.3）：

組合報酬：
μ_p = 0.6 × 9% + 0.4 × 6% = 7.8%

組合風險：
σ_p = √(0.6² × 22² + 0.4² × 16² + 2 × 0.6 × 0.4 × 22 × 16 × 0.3)

詳細計算：

• 第一項：0.36 × 484 = 174.24
• 第二項：0.16 × 256 = 40.96
• 第三項：2 × 0.6 × 0.4 × 22 × 16 × 0.3 = 50.688
• 總和：174.24 + 40.96 + 50.688 = 265.888
• 開根號：√265.888 ≈ 16.31%

震撼結果

對比分析：

• 100% 0050：報酬9%，風險22%
• 100% 00713：報酬6%，風險16%
• 60/40組合：報酬7.8%，風險16.31%

邊際效率：相較100% 00713，60/40組合的風險僅增加0.31個百分點、報酬提升1.8個百分點，邊際報酬/邊際風險≈5.8。這正是前緣「凸性」帶來的配置效率。

這就是效率前緣的威力：透過適當的資產配置，我們可以在幾乎不增加風險的情況下，大幅提升報酬。

相關係數情境敏感度

情境敏感度（以60% 0050／40% 00713為例）

相關係數情境	組合風險	風險差異
ρ = 0.0	14.67%	理想分散
ρ = 0.3	16.31%	正常市況
ρ = 0.6	17.79%	危機期間

啟示：同一組合在「危機相關性上升」時風險顯著抬升，投資組合配置需做壓力測試。

處方：在高相關regime（ρ↑）下，提高債券/防禦資產比例或增加與股市低相關資產（如長天期公債、部分商品/黃金）以維持前緣外凸。

為什麼會有這種效果？

關鍵在於我們第四篇學過的相關係數。當兩個資產的相關係數小於+1時（本例為0.3），它們的價格變動不會完全同步，因此組合後的整體風險會被「分散」掉一部分。

這就是數學上的黃金平衡：1+1可以大於2，也可以小於2，關鍵在於如何組合。

效率前緣上的所有可能性

效率前緣不只是一個點，而是一條完整的曲線，每個點都代表不同的風險報酬組合。

完整的效率前緣曲線

以我們的0050和00713組合為例，不同權重會產生不同的效率點：

0050權重	00713權重	組合報酬	組合風險	解讀
0%	100%	6.0%	16.00%	效率前緣左端
28%	72%	6.84%	14.60%	最小變異數組合（風險最低點）
60%	40%	7.8%	16.31%	效率前緣中段
80%	20%	8.4%	18.81%	效率前緣右段
100%	0%	9.0%	22.00%	效率前緣右端

最小變異數組合：投資組合優化的特殊點

💡 最小變異數組合（MVP）

定義：效率前緣上風險最低的投資組合

在不允許賣空前提下的計算公式：
w* = (σ₂² – ρσ₁σ₂) / (σ₁² + σ₂² – 2ρσ₁σ₂)

本例計算：
w* = (16² – 0.3×22×16) / (22² + 16² – 2×0.3×22×16) = 150.4 / 528.8 ≈ 28.44%

最佳配置：28% 0050 + 72% 00713，組合風險≈14.60%

特性：

• 風險比任何單一資產都低
• 適合極度保守的投資人
• 報酬不是最高，但風險效率最好
• 體現了分散投資的凸性收益

效率前緣的邊界與形狀

左邊界：最小變異數組合，風險無法再降低
右邊界：追求最高報酬的極限
曲線特性：向外凸出，體現分散投資的「凸性收益」

每個投資人最終都會在這條曲線上選擇一個點，但選哪個點，就涉及個人的風險偏好了。

如何估計投資組合優化的關鍵參數

為了讓讀者能實際應用效率前緣概念，這裡提供參數估計的標準作業程序：

參數估計SOP

預期報酬率估計：

1. 歷史平均法：使用最近3-5年的年化平均報酬
2. CAPE隱含報酬法：基於本益比估算合理報酬預期
3. 建議：兩種方法對照，取保守估計值

波動率估計：

1. 資料來源：最近3-5年的月度報酬率數據
2. 計算方法：月度標準差 × √12 = 年化波動率
3. 調整：可考慮危機期間數據的權重調整

相關係數估計：

1. 基礎計算：使用月度對數報酬率計算相關性
2. 壓力測試：危機期間相關係數通常上升，需要情境分析
3. 定期更新：市場結構變化會影響相關性，建議季度檢視

更新頻率建議

建議每季更新相關係數、每半年更新波動、每年重估報酬假設，並做一次壓力測試。

實務注意事項

參數不確定性：歷史數據不能保證未來表現，需要敏感度分析
模型限制：效率前緣基於歷史統計，無法預測黑天鵝事件
動態調整：市場環境變化時，需要重新估計參數和調整配置

效率前緣的深層啟示

打破傳統投資迷思

迷思一：「高報酬必然高風險」
效率前緣告訴我們：透過適當組合，可能在相同風險下獲得更高報酬。

迷思二：「分散就是買更多檔股票」
真正的分散是降低相關性，而非增加數量。兩檔低相關的資產可能比十檔高相關的股票更有效。

迷思三：「投資沒有標準答案」
雖然個人最適解不同，但數學上的最有效率組合是客觀存在的。

投資決策的科學化

效率前緣將資產配置從藝術變成科學：

• 量化比較：不同投資組合配置可以精確計算和比較
• 客觀標準：有明確的數學標準判斷配置效率
• 系統化流程：投資決策可以遵循系統化的分析方法

現代金融理論的基石

效率前緣是許多重要金融理論的出發點：

• 資本資產定價模型（CAPM）：以效率前緣為基礎，導出市場組合與風險溢酬
• 套利定價理論（APT）：與CAPM並列的資產定價框架，強調多因子線性解釋，與效率前緣相關但獨立
• 因子投資：以規模、價值、品質、動能等因子，嘗試將組合推向更有效率的前緣

若加入無風險利率，可從無風險點畫資本市場線，其與效率前緣的切點＝切線組合（夏普比率最大）；細節將在第六篇展開。

立即行動指引：三步驟投資組合效率自檢

第一步：相關性檢視

相關性熱力圖檢查：

• 你的持股是否在相關性熱力圖上呈現相同顏色？
• 如果大部分持股都高度相關（>0.7），表示過度同質化
• 目標：尋找相關係數<0.5的資產組合

第二步：集中度風險評估

單一資產權重檢查：

• 任何單一資產是否超過總投資組合的25%？
• 單一產業或地區是否超過50%？
• 目標：避免過度集中，分散風險暴露

第三步：凸性收益驗證

組合效率檢驗：

• 你的投資組合風險報酬點是否落在兩個主要資產的「內插線」之外？
• 如果組合只是個別資產的線性組合，就沒有獲得分散效益
• 目標：確保組合具有效率前緣的「凸性收益」

簡易效率檢核清單

✓ 相關性：主要持股間相關係數<0.7 ✓ 分散度：無單一資產>25%權重
✓ 跨類別：涵蓋不同資產類別（股債金REITs）
✓ 再平衡：季度檢視並調整偏離目標配置
✓ 參數更新：年度重新估計預期報酬、風險、相關性

需要試算？

下載本文附的效率前緣Excel範本（含MVP與情境切換）。

為下一篇做準備

效率前緣給了我們所有的最佳選項，但如何選擇最適合自己的那個點？這就是我們下一篇要討論的核心問題：個人化的投資組合選擇。

在第六篇中，我們將學習：

• 如何評估個人風險承受度
• 不同生命階段的最適配置
• 無差異曲線與效率前緣的交點分析

常見問題解答

效率前緣是什麼？

效率前緣是給定資產組合下，所有風險-報酬組合中最有效率的點所形成的曲線，每個點都代表相同風險下的最高報酬，或相同報酬下的最低風險。

最小變異數組合適合誰？

適合極度保守的投資人，如即將退休或已退休族群。這個組合提供了所有可能配置中的最低風險，雖然報酬不是最高，但風險效率最好。

60/40是萬靈丹嗎？

不是。60/40組合的效果高度依賴相關係數情境。在正常市況（ρ=0.3）下效果良好，但在危機期間相關性上升（ρ=0.6）時，風險會顯著增加，需要動態調整。

結論

效率前緣徹底改變了我們對投資組合的認知。它告訴我們：

最佳投資組合不是憑感覺，而是有數學解：每種配置的效率都可以客觀計算和比較。

分散投資的真正意義：不是買更多檔股票，而是降低資產間的相關性。

風險報酬的最佳平衡：透過數學最佳化，可以找到每個風險水平下的最高報酬組合。

投資決策的科學基礎：現代投資組合理論為量化投資決策提供了堅實的數學基礎。

效率前緣是一個工具，不是答案。真正的答案在於如何運用這個工具，找到最適合自己的投資策略。這正是我們下一篇要深入探討的主題。

記住：市場充滿不確定性，但投資組合的效率是可以計算和優化的。掌握效率前緣，就掌握了科學投資的核心邏輯。

---

系列文章導航

• 第一篇：投資組合的誕生：從直覺到科學的革命
• 第二篇：用數學量化時間價值：從複利與現值看穿投資的真實代價
• 第三篇：投資風險怎麼算？用標準差與變異數量化波動
• 第四篇：分散投資真的有效嗎？相關係數揭露投資組合的真實風險
• 第五篇：最佳投資組合怎麼找？效率前緣教你報酬與風險的黃金平衡（本篇）
• 第六篇：我的投資組合怎麼配？找到效率前緣上的最適解（即將發布）

免責聲明：效率前緣是重要的投資分析工具，但基於歷史數據的分析不能保證未來表現。市場環境會持續變化，投資人應該定期檢視和調整投資組合。本文僅供教育參考，任何投資決定都應該基於你自己的研究和風險承受能力。投資有風險，決策須謹慎。